soal fungsi : kuadrat, rasional, irasional

Nama : Refika Rachmawaty

Kelas : X IPS

No Absen : 28

SOAL KUADRAT, RASIONAL, IRASIONAL

SOAL KUADRAT

1. f(x) = 4x² + 3x + 8. Hitunglah nilai a + 2b + 3c!

Jawaban:

Diketahui nilai a = 4, b = 3, c = 8
= a + 2b + 3c
= 4 + 2(3) + 3(8)
= 4 + 6 + 24
= 34

2. f(x) = 3x² - 2x + 5 memiliki bentuk sesuai dengan bentuk f(x) = ax² + bx + c. Hitunglah nilai 2a + 3b + 4c!

Jawaban:

= Diketahui nilai a = 3, b = -2, c = 5
= 2a + 3b + 4c
= 2(3) + 3(-2) + (4 x 5)
= 6 - 6 + 20
= 20

3. Diketahui fungsi f(x) = x² + 4x + 5. Hitunglah bayangangan untuk nilai x = 3

Jawaban:
= f(x) = x² + 4x + 5
= f(3) = 3² + 4(3) + 5
= f(3) = 9 + 12 + 5
= f(3) = 26

DAFTAR PUSAKA : https://www.detik.com/edu/detikpedia/d-5737885/contoh-soal-fungsi-kuadrat-lengkap-dengan-pembahasan

4. Nilai a, b dan c dari fungsi f(x)=-2x²+3(2x+5) adalah....

a. 2, 5 dan 8

b. -2, 3 dan 5

c. -2, 6 dan 5

d. -2, 6 dan 15

Pembahasan :

f(x)=-2x²+3(2x+5)

= -2x² + 6x + 15

maka a=-2, b=6 dan c=15

5. Nilai f(-3) dari fungsi f(x)=x²-4x+2 adalah...

a. -1

b. 1

c. 5

d. 23

Pembahasan :

f(x) =x²-4x+2

f(-3)=(-3)²-4(-3)+2

=9 + 12 + 2

=23
6. Fungsi f(x)=x²- 5x + 6 memotong sumbu y di titik...

a. (0,-5)

b. (0,6)

c. (-5,0) d. (6,0)

Pembahasan :

Titik potong dengan sumbu ya di dapat jika x=0, maka

f(0)=0²- 5(0) + 6

x=0 dan y=6

titik potong (0,6)

7. Fungsi kuadrat yang sumbu simetrinya sumbu y adalah...

a. y=x² - 9

b. y=x² + 7x + 12

c. y=x² -5x d. y=(x - 4)²

Pembahasan :

Sumbu y berarti x=0

karena persamaan sumbu simetri adalah x=-b/2a, maka b=0

yang nilai b=0 adalah pilihan a. y=x² - 9

8. Fungsi kuadrat yang tidak memotong sumbu x adalah...

a. y=x² - 5x - 14

b. y=x² - 25

c. y=2x² + 5x + 3 d. y=3x² - 7x + 5

Pembahasan :

D > 0, memotong sumbu x di dua titik

D=0, menyinggung sumbu x di satu titik

D < 0, tidak memotong sumbu x

a. y=x² - 5x - 14, nilai a=1, b=-5, c=-14

D=b² - 4.a.c =(-5)² - 4.1.-14

=81 (memotong di dua titik)

b. y=x² - 25, nilai a=1, b=0, c=-25

D=0² - 4.1.-25

=100 (memotong di dua titik)

c. y=2x² + 5x + 3, nilai a=2, b=5, c=3

D=5² - 4.2.3

=1 (memotong di dua titik

d. y=3x² - 7x + 5, nilai a=3, b=-7, c=5

D=-7² - 4.3.5

=-11 (tidak memotong sumbu x)

9. Fungsi f(x)=x² - 8x + 12 memotong sumbu x di titik ....

a. (-8,0) dan (12,0)

b. (8,0) dan (-12,0)

c. (2,0) dan (6,0) d. (-2,0) dan (-6,0)

Pembahasan :

memotong sumbu x, nilai fungsi=0

x² - 8x + 12=0

(x - 2) (x - 6)=0

x - 2=0 dan x - 6=0

x =2 dan x =6 titik (2,0) dan (6,0)

10. Persamaan sumbu simetri fungsi y=3(x -5)² - 40 adalah...

a. x=-10

b. x=-5

c. x=5 d. x=10

Pembahasan :

y=3(x -5)² - 40

=3(x²-10x+25) - 40

=3x² - 30x + 75 - 40

DAFTAR PUSAKA : https://www.edukasi.site/2019/09/soal-fungsi-kuadrat-kelas-9.html

SOAL RASIONAL

1. Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Untuk y = 1/x dalam kuadran III,

Mendeskripsikan sifat dari ujung grafik fungsi tersebut.
Mendeskripsikan apa yang akan terjadi pada saat x mendekati nol.

Pembahasan Serupa dengan sifat grafiknya pada kuadran I, maka akan kita peroleh

Pada saat x mendekati negatif tak hingga, nilai y akan mendekati nol. Jika disimbolkan akan menjadi: x → –∞, y → 0.
Pada saat x mendekati nol dari kiri, nilai y akan mendekati negatif tak hingga. Pernyataan tersebut juga bisa kita tuliskan dengan simbol x → 0–, y → –∞.

Fungsi y = 1/x²

Dari pembahasan di atas, kita bisa mengetahui bahwa grafik dari fungsi ini akan mengalami jeda pada saat x = 0.

Namun demikian, sebab kuadrat dari sembarang bilangan negatif merupakan bilangan positif, cabang-cabang dari grafik fungsi ini akan terletak kdi atas sumbu-x.

Perhatikan bahwa fungsi y = 1/x² adalah fungsi genap.

rasional dan grafiknya pdf

Sama halnya dengan y = 1/x, nilai x yang mendekati positif tak hingga akan menghasilkan y yang mendekati nol. Jika kita tulis simbolnya maka akan menjadi: x → ∞, y → 0.

Hal ini adalah salah satu indikasi dari sifat asimtot dalam arah horizontal. Serta kita akan menyatakan y = 0 adalah asimtot horizontal dari fungsi y = 1/x dan y = 1/x². Secara umum,

Asimtot Horizontal
Diberikan sebuah konstanta k, garis y = k adalah asimtot horizontal dari fungsi V(x) apabila x bertambah tanpa batas, akan menimbulkan V(x) mendekati k: x → –∞, V(x) → k atau x → ∞, V(x) → k.

Pada gambar (a) di bawah ini menggambarkan garis asimtot horizontal pada y = 1, yang menunjukan grafik f(x) sebagai translasi grafik y = 1/x ke atas sejauh 1 satuan.

Gambar (b) menggambarkan garis asimtot horizontal pada y = –2, yang menunjukan grafik g(x) sebagai pergeseran grafik y = 1/x² ke bawah sejauh 2 satuan.

integral rasional

Contoh 2

Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Berdasarkan gambar (b) di atas, pakailah notasi matematika guna:

Mendeskripsikan sifat dari ujung grafik di atas.
Mendeskripsikan apa yang berlangsung pada saat x mendekati nol.

Pembahasan

Pada saat x → –∞, g(x) → –2. Ketika x → ∞, y → –2.
Pada saat x → 0–, g(x) → ∞. Ketika x → 0+, y → ∞.

Dari contoh 2b di atas, maka dapat diketahi bahwasannya pada saat x mendekati nol, g akan berubah menjadi sangat besar serta semakin bertambah tidak terbatas.

Hal tersebut adalah indikasi dari sifat asimtot dalam arah vertikal.

Dan kemudian kita akan menyebut garis x = 0 adalah asimtot vertikal untuk g (x = 0 juga adalah asimtot vertikal untuk f). Secara umum,

Asimtot Vertikal
Diberikan sebuah konstanta h, garis x = h adalah asimtot vertikal untuk fungsi V apabila x mendekati h, V(x) akan bertambah atau berkurang tanpa batas: pada saat x → h+, V(x) → ±∞ atau pada saat x → h–, V(x) → ±∞.

Mengidentifikasi dari asimtot horizontal dan vertikal sangatlah bermanfaat.

Sebab grafik y = 1/x dan y = 1/x² bisa ditransformasi dengan menggesernya ke arah vertikal maupun gorizontal. Fungsi,

adalah bentuk pergeseran dari fungsi y = 1/x. Sementara untuk fungsi,

adalah bentuk pergeseran dari fungsi y = 1/x²

Contoh 3

Menuliskan Persamaan dari Fungsi Rasional

Identifikasi fungsi yang diberikan oleh grafik pada gambar di bawah, lalu pakailah grafik tersebut untuk menuliskan persamaan fungsi tersebut. Anggaplah |a| = 1.

asimtot

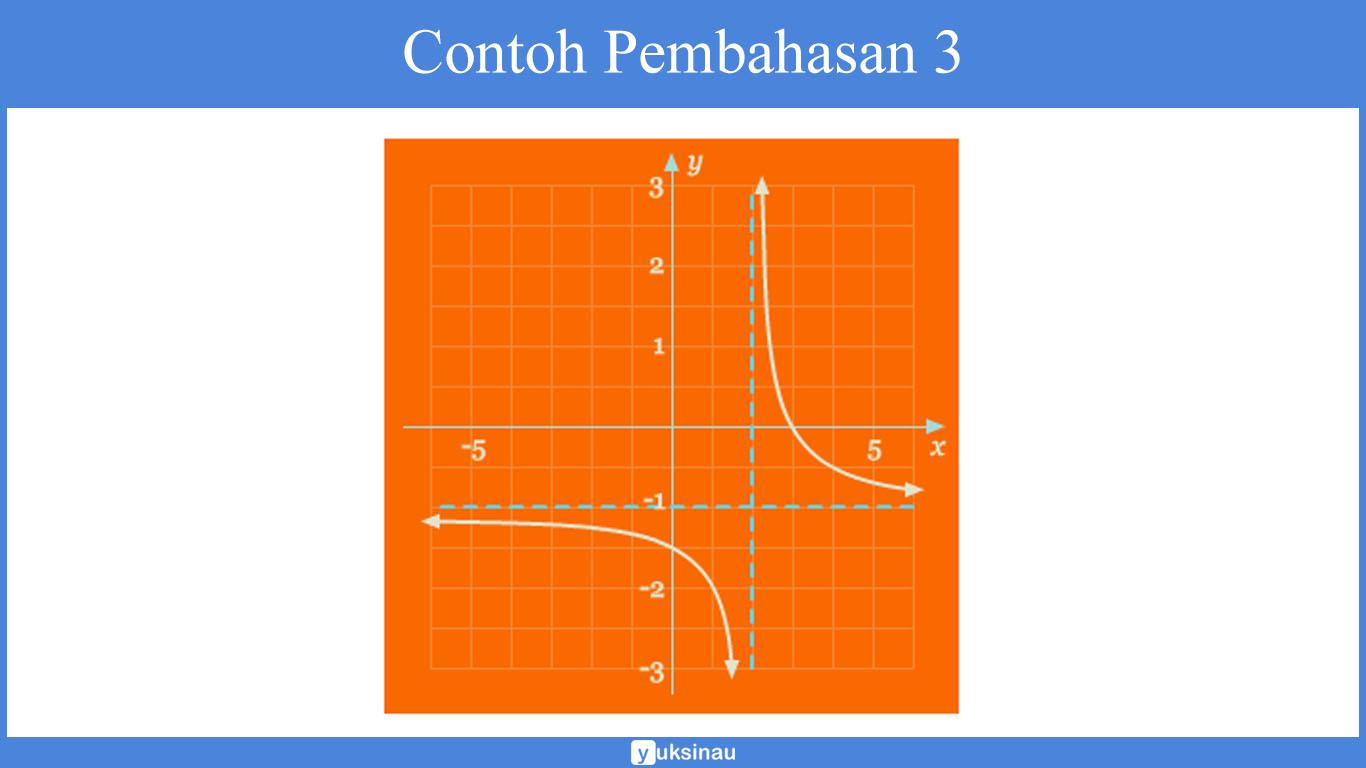
Pembahasan dari grafik di atas, dapat kita ketahui bahwasannya grafik tersebut adalah pergeseran dari fungsi y = 1/x ke kanan sejauh 2 satuan. Serta bergeser ke bawah sejauh 1 satuan.

Sehingga asimtot horizontal serta vertikal dari grafik di atas secara berturut-turut yaitu y = –1 dan x = 2. Maka dari itu, persamaan dari grafik di atas yaitu:

yang mana adalah bentuk dari pergeseran fungsi y = 1/x.

DAFTAR PUSAKA : https://www.yuksinau.id/fungsi-rasional/

SOAL IRASIONAL

1. Kuadratkan kedua ruas pada pertidaksamaan irasional berupa x² – 6x – 7 < x² – 4x + 3?

Jawab.
Cara menghitung pertidaksamaan irasional yang pertama yaitu menyelesaikan pertidaksamaannya terlebih dahulu. Maka:
x² – 6x – 7 < x² – 4x + 3
x² – 6x – 7 – x² + 4x – 3 < 0
-2x – 10 < 0
2x + 10 > 0 (semua ruas dikalikan -1)
2x > -10
x > -5

Langkah penyelesaian contoh soal pertidaksamaan irasional selanjutnya yaitu memenuhi syarat pertama (≥ 0) dan mengubahnya dalam bentuk harga nol. Sehingga hasilnya menjadi:
x² – 6x – 7 ≥ 0
(x – 7)(x + 1) ≥ 0
x – 7 = 0 atau x + 1 = 0 (diubah menjadi harga nol)
x = 7 atau x = -1

Cara menyelesaikan pertidaksamaan selanjutnya yaitu memenuhi syarat kedua (≥ 0) dan mengubahnya dalam bentuk harga nol. Sehingga hasilnya menjadi:
x² – 4x + 3 ≥ 0
(x – 3)(x -1) ≥ 0
x – 3 = 0 atau x – 1 = 0 (diubah menjadi harga nol)
x = 3 atau x = 1
Jadi himpunan penyelesaiannya ialah {x|-5 < x ≤ 1 atau x ≥ 7}.

DAFTAR PUSAKA : http://www.antotunggal.com/2021/09/pembahasan-contoh-soal-pertidaksamaan-irasional.html