FUNGSI KUADRAT, RASIONAL, IRASIONAL

 Nama  : Refika Rachmawaty                                                                                                                          Kelas   : X IPS 1 / 28

               fungsi kuadrat, rasional dan irasional

Fungsi Rasional

Fungsi Rasional
Fungsi rasional merupakan fungsi yang mempunyai bentuk umum

Dengan p dan d adalah polinomial dan d(x) ≠ 0. Domain dari V(x) merupakan seluruh bilangan real, kecuali pembuat nol dari d.

Adapun fungsi rasional yang paling sederhana, yakni fungsi y = 1/x dan fungsi y = 1/x².

Di mana keduanya mempunyai pembilang konstanta sertaa penyebut polinomial dengan satu suku. Dan kedua fungsi tersebut mempunyai domain semua bilangan real kecuali x ≠ 0.

Fungsi y = 1/x

Fungsi ini disebut juga sebagai fungsi kebalikan sebab setiap kita mengambil sembarang x (kecuali nol) maka akan menghasilkan kebalikannya sebagai nilai dari fungsi tersebut.

Yang artinya x yang besar akan menghasilkan nilai fungsi yang kecil, begitu juga sebaliknya. Tabel dan grafik dari fungsi tersebut bisa dilihat pada gambar di bawah ini.

Tabel dan grafik di atas menunjukan beberapa hal yang menarik.

Yang pertama, grafik tersebut lolos pada uji garis vertikal. Yang berarti setiap garis vertikal pada bidang koordinat Cartesius akan memotong grafik pada maksimal satu titik.

Sehingga, y = 1/x adalah sebuah fungsi.

Yang kedua, sebab pembagian tidak terdefinisi jadi saat pembaginya nol, maka nol tidak akan mempunyai pasangan, sehingga menghasilkan jeda pada x = 0.

Hal tersebut sesuai dengan domain dari fungsi tersebut, yakni seluruh x anggota bilangan real kecuali 0.

Yang ketiga, fungsi tersebut adalah fungsi ganjil, dengan salah satu cabangnya terletak di kuadran I.

Sementara yang lainnya berada pada kuadran III.

Kemudian yang terakhir, pada kuadran I, saat x menuju tak hingga, nilai y menuju dan mendekati nilai nol.

Secara simbolis bisa kit tuliskan sebagai x → ∞, y → 0. Secara grafis, kurva dari grafik fungsi tersebut akan mendekati sumbu-x pada saat x mendekati tak hingga.

Tak hanya itu saja, kita juga bisa mengamati bahwa pada saat x mendekati nol dari kanan maka nilai y akan mendekati bilangan real positif yang sangat besar (positif tak hingga): x → 0+, y → ∞.

Untuk catatan, tanda + atau – yang berada di atas akan mengindikasikan arah dari pendekatan. Yakni dari sisi positif (+) atau dari sisi negatif (–).

Contoh 1

Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Untuk y = 1/x dalam kuadran III,

1. Mendeskripsikan sifat dari ujung grafik fungsi tersebut.
2. Mendeskripsikan apa yang akan terjadi pada saat x mendekati nol.

Pembahasan Serupa dengan sifat grafiknya pada kuadran I, maka akan kita peroleh

1. Pada saat x mendekati negatif tak hingga, nilai y akan mendekati nol. Jika disimbolkan akan menjadi: x → –∞, y → 0.
2. Pada saat x mendekati nol dari kiri, nilai y akan mendekati negatif tak hingga. Pernyataan tersebut juga bisa kita tuliskan dengan simbol x → 0–, y → –∞.

Fungsi y = 1/x²

Dari pembahasan di atas, kita bisa mengetahui bahwa grafik dari fungsi ini akan mengalami jeda pada saat x = 0.

Namun demikian, sebab kuadrat dari sembarang bilangan negatif merupakan bilangan positif, cabang-cabang dari grafik fungsi ini akan terletak kdi atas sumbu-x.

Perhatikan bahwa fungsi y = 1/x² adalah fungsi genap.

Sama halnya dengan y = 1/x, nilai x yang mendekati positif tak hingga akan menghasilkan y yang mendekati nol. Jika kita tulis simbolnya maka akan menjadi: x → ∞, y → 0.

Hal ini adalah salah satu indikasi dari sifat asimtot dalam arah horizontal. Serta kita akan menyatakan y = 0 adalah asimtot horizontal dari fungsi y = 1/x dan y = 1/x². Secara umum,

Asimtot Horizontal
Diberikan sebuah konstanta k, garis y = k adalah asimtot horizontal dari fungsi V(x) apabila x bertambah tanpa batas, akan menimbulkan V(x) mendekati k: x → –∞, V(x) → k atau x → ∞, V(x) → k.

Pada gambar (a) di bawah ini menggambarkan garis asimtot horizontal pada y = 1, yang menunjukan grafik f(x) sebagai translasi grafik y = 1/x ke atas sejauh 1 satuan.

Gambar (b) menggambarkan garis asimtot horizontal pada y = –2, yang menunjukan grafik g(x) sebagai pergeseran grafik y = 1/x² ke bawah sejauh 2 satuan.

Contoh 2

Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Berdasarkan gambar (b) di atas, pakailah notasi matematika guna:

1. Mendeskripsikan sifat dari ujung grafik di atas.
2. Mendeskripsikan apa yang berlangsung pada saat x mendekati nol.

Pembahasan

1. Pada saat x → –∞, g(x) → –2. Ketika x → ∞, y → –2.
2. Pada saat x → 0–, g(x) → ∞. Ketika x → 0+, y → ∞.

Dari contoh 2b di atas, maka dapat diketahi bahwasannya pada saat x mendekati nol, g akan berubah menjadi sangat besar serta semakin bertambah tidak terbatas.

Hal tersebut adalah indikasi dari sifat asimtot dalam arah vertikal.

Dan kemudian kita akan menyebut garis x = 0 adalah asimtot vertikal untuk g (x = 0 juga adalah asimtot vertikal untuk f). Secara umum,

Asimtot Vertikal
Diberikan sebuah konstanta h, garis x = h adalah asimtot vertikal untuk fungsi V apabila x mendekati h, V(x) akan bertambah atau berkurang tanpa batas: pada saat x → h+, V(x) → ±∞ atau pada saat x → h–, V(x) → ±∞.

Mengidentifikasi dari asimtot horizontal dan vertikal sangatlah bermanfaat.

Sebab grafik y = 1/x dan y = 1/x² bisa ditransformasi dengan menggesernya ke arah vertikal maupun gorizontal. Fungsi,

adalah bentuk pergeseran dari fungsi y = 1/x. Sementara untuk fungsi,

adalah bentuk pergeseran dari fungsi y = 1/x². Kemudian perhatikan contoh yang ada di bawah ini:

Contoh 3

Menuliskan Persamaan dari Fungsi Rasional

Identifikasi fungsi yang diberikan oleh grafik pada gambar di bawah, lalu pakailah grafik tersebut untuk menuliskan persamaan fungsi tersebut. Anggaplah |a| = 1.

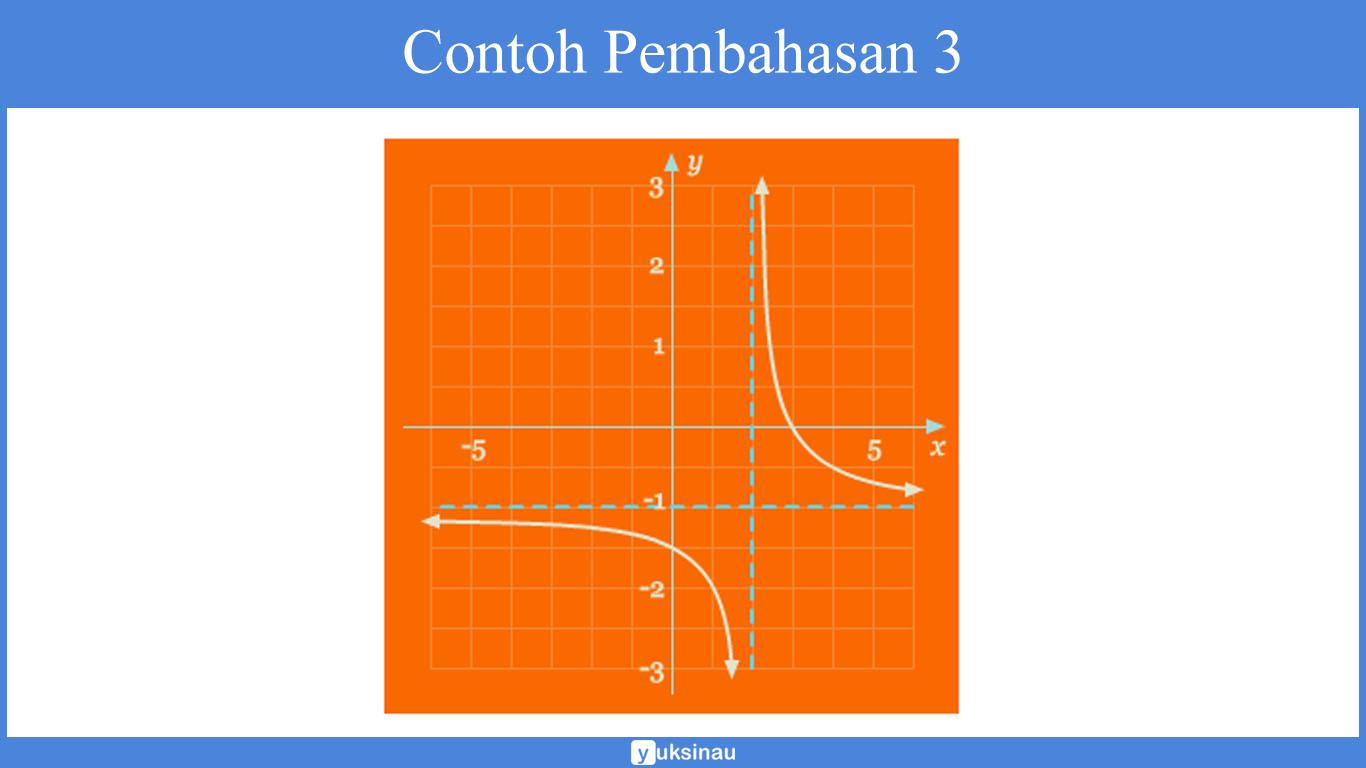
Pembahasan dari grafik di atas, dapat kita ketahui bahwasannya grafik tersebut adalah pergeseran dari fungsi y = 1/x ke kanan sejauh 2 satuan. Serta bergeser ke bawah sejauh 1 satuan.

Sehingga asimtot horizontal serta vertikal dari grafik di atas secara berturut-turut yaitu y = –1 dan x = 2. Maka dari itu, persamaan dari grafik di atas yaitu:

yang mana adalah bentuk dari pergeseran fungsi y = 1/x.

DAFTAR PUSAKA : https://www.yuksinau.id/fungsi-rasional/

FUNGSI RASIONAL 

Fungsi kuadrat atau yang dikenal juga sebagai fungsi polinom adalah fungsi dengan pangkat peubah tertingginya adalah 2.

Pada umumnya, bentuk umum dari fungsi kuadrat adalah f(x)=ax2+bx+c atau y=ax2+bx+c.

Suatu fungsi selalu berkaitan dengan grafik fungsi. Begitu juga dengan yang ada pada fungsi kuadrat.

Grafik fungsi kuadrat memiliki bentuk seperti parabola. Untuk menggambar grafik fungsi kuadrat harus ditentukan titik potong dengan sumbu koordinat dan juga titik ekstrim.

Adapun sebutan lain untuk titik ekstrim yaitu titik puncak atau titik maksimum atau minimum. Dan sekarang kita membasa masing-masing dari titik tersebut. Simak pembahasannya berikut ini.

Titik Potong dengan Sumbu Koordinat

Titik potong dengan sumbu X didapatkan dengan cara menentukan nilai peubah x pada fungsi kuadrat. Apabila nilai peubah y sama dengan nol, sehingga akan didapatkan titik potong (x1,0) dan (x2,0).

Yang mana x1 dan x2 adalah akar-akar persamaan kuadrat.

Namun perlu kalian ingat bahwasannya berbagai akar persamaan kuadrat tergantung dari diskriminannya.

Apabila diskriminannya sama dengan nol maka akan didapatkan hanya satu akar dan ini berarti hanya ada satu titik potong dengan sumbu X.

Jika nilai diskriminannya kurang dari nol persamaan kuadrat tersebut tidak mempunyai akar real yang berarti tidak mempunyai titik potong dengan sumbu X.

Titik potong dengan sumbu Y didapatkan dengan cara mencari nilai y pada fungsi kuadrat apabila nilai peubah x sama dengan nol, sehingga akan didapatkan titik (0,y1).

Titik Ekstrim

Titik ekstrim pada fungsi kuadrat adalah sebuah koordinat dengan absisnya merupakan nilai sumbu simetri serta ordinatnya adalah nilai ekstrim.

Pasangan koordinat titik ekstrim pada fungsi kuadrat y=ax2+bx+c yaitu seperti berikut ini.

D merupakan diskriminan

D=b2-4ac

Seperti yang telah kita sebutkan di atas,

  merupakan sumbu simetri dan  adalah nilai ekstrim dari fungsi kuadrat.

Pembuktian Rumus Titik Ekstrim Fungsi Kuadrat

Titik ekstrim dapat kita peroleh dari konsep turunan pertama.

Titik ekstrim fungsi kuadrat y=ax2 + bx + c didapatkan dengan cara menurunkannya terlebih dahulu, lalu hasil turunannya sama dengan nol, y’ = 0, sehingga akan didapatkan bentuk seperti di bawah ini:

Berikut adalah tahapan untuk menggambar grafik fungsi kuadrat y=ax2+bx+c

1. Menentukan titik potong dengan sumbu koordinat.
   • Titik potong dengan sumbu X apabila y=0.
     (tidak ada untuk fungsi kuadrat yang mempunyai D<0).
   • Titik Potong dengan sumbu Y apabila x=0.
2. Tentukan titik ekstrim, yakni

Contoh soal:

Mari kita bedah bersama fungsi kuadrat dari f(x)=x2-6x+8

Titik potong dengan sumbu X 

Ingat titik potong dengan sumbu X akan didapatkan apabila nilai y=0, maka dari itu akan didapatkan bentuk persamaan kuadrat x2-6x+8=0.

Untuk memastikan bahwa persamaan kuadrat di atas mempunyai akar, maka langkah pertama adalah menentukan terlebih dahulu diskriminannya.

D=b2-4ac=(-6)2-4(1)(8)=36-32=4

Sebab diskriminannya 4 (positif) pastilah persamaan kuadratnya mempunyai dua akar real berbeda.

Hal itu berarti, fungsi kuadrat di atas mempunyai dua titik potong dengan sumbu X. Titik potong dengan sumbu X didapatkan dari akar-akar persamaan kuadrat.

x2-6x+8=0
(x-2)(x-4)=0
x=2 atau x=4

Sehingga, titik potong dengan sumbu X yaitu (2,0) dan (4,0)

Titik Potong dengan Sumbu Y 

Titik potong dengan sumbu Y akan didapatkan apabila nilai x=0.
y=x2-6x+8
y=02-6(0)+8=8

Sehinga, titik potong dengan sumbu Y yaitu (0,8)

Titik Ekstrim 

Titik ekstrim fungsi kuadrat f(x)=ax2+bx+c yaitu

Artinya untuk fungsi kuadrat f(x)=x2-6x+8 titik ekstrimnya ialah seperti di bawah ini:

Sumbu simetrinya yaitu x=3 dan nilai ekstrimnya yakni -1.

Dari informasi titik potong dengan sumbu X, titik potong dengan sumbu Y, dan juga titik ekstrim dapat kita gambar grafik fungsi kuadratnya.

Tahapannya, sesudah mendapatkan titik potong dengan sumbu X, titik potong dengan sumbu Y, dan juga titik ekstrim. Lalu gambarkan titik-titik itu pada koordinat kartesius kemudian hubungkan dengan kurva halus.

Pada contoh soal di atas, fungsi kuadrat f(x)=x2-6x+8 mempunyai titik potong dengan sumbu X (2,0) dan (4,0), titik potong dengan sumbu Y (0,8) serta titik ekstrim (3,-1).

Gambar dari titik-titik ini pada koordinat kartesius ada pada gambar di bawah ini.

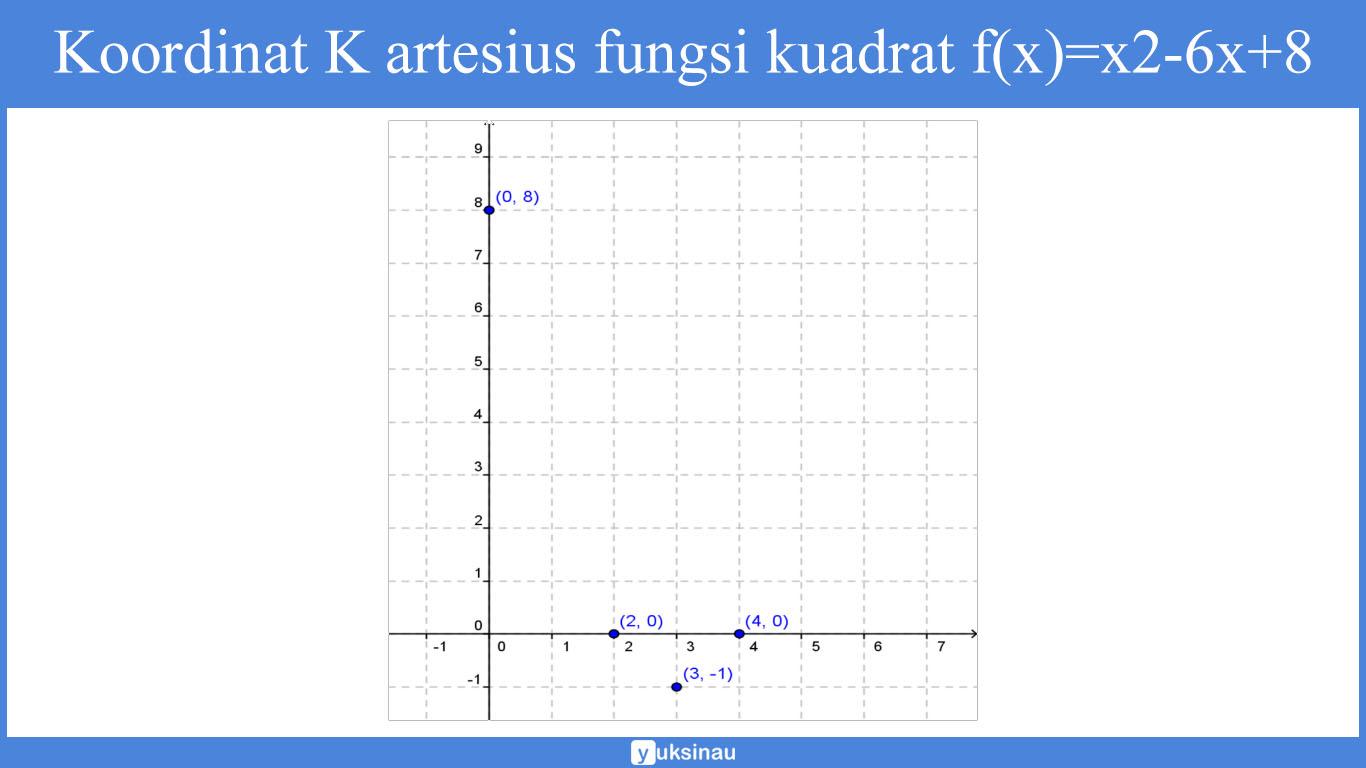
Kemudian hubungkan titik-titik tersebut dengan satu kurva halus, sehingga akan didapatkan kurva fungsi kuadrat f(x)=x2-6x+8 seperti berikut ini:

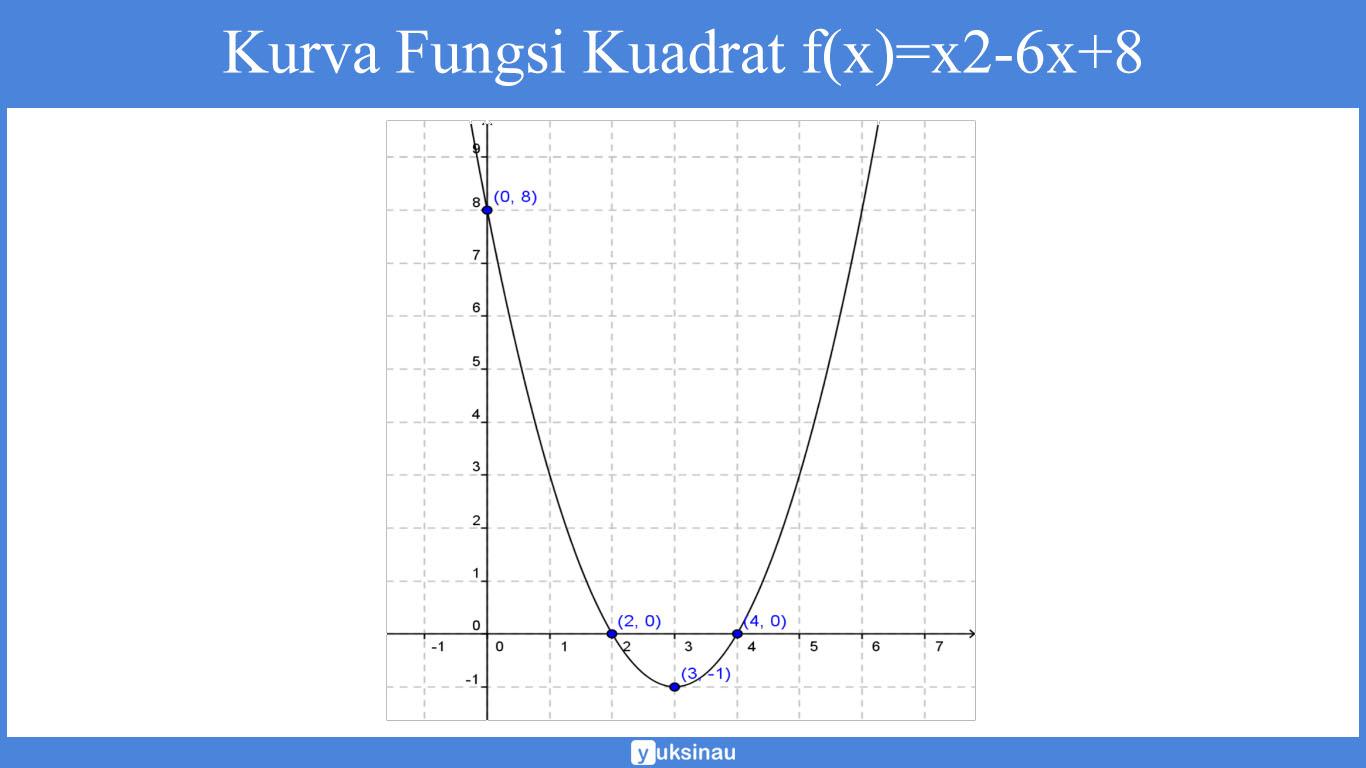
Sifat Kurva Parabola

1. Berdasarkan koefisien “ɑ”

Nilai a memiliki fungsi sebagai penentu arah membukanya suatu grafik.

• Apabila a > 0, parabola terbuka ke atas sementara titik baliknya minimum sehingga memiliki nilai minimum.
• Apabila a < 0, parabola terbuka ke bawah sementara titik baliknya maksimum sehingga memiliki nilai maksimum.

2. Berdasarkan koefisien “b”

Nilai b memiliki fungsi sebagai penentu untuk menentukan posisi sumbu simetri yang ada pada grafik.

• Untuk a dan b bertanda sama (a > 0, b > 0) atau (a < 0, b <0) maka, sumbu simetri posisinya ada di kiri sumbu y.
• Untuk a dan b berlainan tanda (a < 0, b > 0) atau (a > 0, b < 0) maka, sumbu simetri posisinya ada di kanan sumbu y.

3. Berdasarkan koefisien “c”

Nilai c memiliki fungsi sebagai penentu titik potong dengan sumbu y.

• Apabila c > 0, grafik parabola memotong di sumbu y positif.
• Apabila c < 0, grafik parabola memotong di sumbu y negatif.

4. Berdasarkan D = b2 – 4ac (diskriminan)

• Apabila D > 0 persamaan kuadrat memiliki dua akar real yang berlainan.
  Parabola akan memotong sumbu x di dua titik. Untuk D kuadrat sempurna maka kedua akarnya rasional, sementara D tidak berbentuk kuadrat sempurna maka kedua akarnya berupa akar irasional.
• Apabila D = 0 persamaan kuadrat memiliki dua akar yang sama (akar kembar), real, dan juga rasional. Parabola akan menyinggung pada sumbu x.
• Apabila D < 0 persamaan kuadrat tidak memiliki akar real atau kedua akarnya tidak real (imajiner). Parabola tidak akan memotong serta tidak akan menyinggung di sumbu x.
  • Untuk D < 0, a > 0 parabola akan selalu berada di atas sumbu x atau biasa disebut sebagai definit positif.
  • Untuk D < 0, ɑ < 0 parabola akan selalu berada di bawah sumbu x atau biasa disebut sebagai definit negatif.

Menyusun Fungsi kuadrat

1. Jika memotong pada sumbu x di (x1,0) dan (x2,0), maka rumus yang berlaku yaitu: y = ƒ (x) = ɑ (x – x1) (x – x2).
2. Jika titik puncak (xp, yp) maka rumus yang berlaku yaitu: y = ƒ (x) = ɑ (x – xp)2 + yp.
3. Jika menyinggung sumbu x di (x1,0) maka rumus yang berlaku yaitu: y = ƒ (x) = ɑ (x – x1)2

Hubungan Garis Dengan Parabola

Berdasarkan D = b2 – 4ac, kedudukan garis pada parabola dibagi menjadi 3 macam, antara lain:

1. D > 0 berarti garis akan memotong parabola ada di dua titik.
2. D = 0 berarti garis memotong parabola di satu titik (menyinggung)
3. D < 0 berarti garis tidak memotong dan tidak akan menyinggung parabola.

Contoh Soal dan Pembahasan

Soal 1:

Apabila fungsi f(x)=px2-(p+1)x-6 mencapai nilai tertinggi untuk x=-1, maka tentukan nilai p.

Jawab:

x=-1 merupakan sumbu simetri, rumusnya -b/2a.

Artinya: -b/2a=-1
-(-(p+1))/2(p)=-1
p+1=-2p
3p=-1
p=-1/3

Soal 2: 

Menentukan titik ekstrim dan juga titik potong dengan sumbu X untuk fungsi kuadrat
f(x)=x2-20x+75.

Jawab:
Titik ekstrim rumusnya:

Titik potong dengan sumbu X apabila y=0 untuk fungsi kuadrat y=x2-20x+75 titik ekstrimnya:

Titik potong dengan sumbu X

x2-20x+75=0
(x-5)(x-15)=0
x=5 atau x=15 sehingga titik potongnya adalah (5,0) dan (15,0)

Soal 3:
Koordinat titik balik grafik fungsi kuadrat y=x2+4x-6 yaitu…

Jawab:

Koordinat balik rumusnya yaitu:

Advertisement

Soal 4: 

Diketahui f(x) = -x2 + 5x + c, apbila ordinat puncaknya 6 maka nilai c yaitu…

Jawab:

Ordinat titik puncak, rumus: -D/4a
-(52-4(-1)c)/4(-1) = 6
-(25+4c)/-4=6
-(25+4c)=-24
25+4c=24
4c=-1
c=-1/4

Selanjutnya akan kami berikan contoh soal pada SNMPTN dan juga UN mengenai fungsi kuadrat, simak baik-baik pembahasan di bawah ini:

Soal 1. (MADAS SNMPTN 2012)

Jika gambar di bawah ini adalah grafik fungsi kuadrat f dengan titik puncak (-2,0) dan melalui titik (0,-4) maka nilai f(-5) adalah …

1. -7
2. -8
3. -9
4. -10
5. -11

Jawab:

Diketahui titik puncak ( xp , yp) = (-2,0), melewati titik (x , y) = (0,-4)

Rumus yang sesuai jika diketahui titik puncaknya adalah:

y = f(x) = a(x-xp )2 + yp

Untuk mencari nilai a, maka:

y = f(x) = a(x-xp)2 + yp
y = a(x+2)2 + 0
-4 = a(0+2)2 + 0
-4 = 4a
a = -1

Sehingga akan diperoleh:
f(x) = -(x + 2)2, dengan f(-5)
f(-5) = -(-5 + 2)2 = -9

Jadi, jawabannya yaitu: C

Soal 2. (MatDas SBMPTN 2013)

Jika grafik fungsi kuadrat f(x) = ax2 + bx + c mempunyai titik puncak (8,4) dan memotong sumbu-x negatif maka …

1. a > 0, b > 0 dan c > 0
2. a < 0, b < 0 dan c > 0
3. a < 0, b > 0 dan c < 0
4. a > 0, b > 0 dan c < 0
5. a < 0, b > 0 dan c > 0

Jawab:

Diketahui titik puncaknya adalah (8,4), sehingga grafik terbuka ke bawah, maka:

a < 0
xp = -b/2a = 8, karena a < 0 → b > 0
D = b2 – 4ac, syarat memotong sumbu x negatif D > 0 sebab b > 0 dan a < 0, maka:
b2 – 4ac > 0
(+) – 4(-)c > 0
c > 0

Jadi jawabannya yaitu: E

Soal 3. (Matematika IPA SBMPTN 2014)

Diketahui suatu parabola simetris terhadap garis x = -2 dan garis singgung parabola tersebut dititik (0,1) sejajar dengan garis 4x + y = 4 . Titik puncak parabola tersebut adalah …

1. (-2,-3)
2. (-2,-2)
3. (-2,0)
4. (-2,1)
5. (-2,5)

Jawab: 

Misalkan persamaan parabolanya adalah  y = ax2 + bx + c parabola simetris kepada garis xp = -2 maka tentukan xp = -b/2a =-2 → b = 4

garis ≡ 4x+y = 4 → mg = -4
Sebab sejajar  maka mparabola = mgaris = -4
mparabola = y
2ax + b = -4 lewat titik (0,1)
2a(0) + b = -4
b = -4

Untuk menentukan xp dan yp:
b = 4a
-4 = 4a
a = -1

Persamaan parabola y = ax2 + bx + c adala:h sebagai berikut
y = -x2 – 4x + c melalui titik (0,1)
1 = -02 – 4(0) + c
c = 1

Maka bisa dihitung y = -x2 – 4x + 1
xp = -b/2a = -(-4)/2(-1) = -2 dan yp = -(-2)2 – 4(-2) +1= 5

Sehingga titik puncak parabolanya yaitu (-2,5)

Jadi jawabannya yaitu: E

Soal 4. (UN 2008)

Persamaan grafik fungsi kuadrat yang melalui titik A(1,0), B(3,0), dan C(0,-6) adalah 

1. y = 2x2 + 8x – 6
2. y = -2x2 + 8x – 6
3. y = 2x2 – 8x + 6
4. y = -2x2 – 8x – 6
5. y = -x2  + 4x – 6

Jawab:

Untuk titik C (0,-6) → x = 0, y = – 6

Untuk titik A (1,0) dan B (3,0) → x1 = 1, x2 = 3

Maka rumus yang berlaku adalah y = a(x – x1)(x – x2)

y = a(x – 1)(x – 3)
– 6 = (0 – 1)(0 – 3)
– 6 = 3a
a = – 2

Menentukan fungsi kuadrat caranya:

y = a(x – x1)(x – x2)
y = – 2(x – 1)(x – 3)
y = – 2(x2 – 4x + 3)
y = – 2x2 + 8x – 6

Jadi jawabannya yaitu: B

Soal 5. (UN 2007)

Perhatikan gambar!

Persamaan grafik fungsi kuadrat pada gambar adalah …

1. y = -2x2 + 4x + 3
2. y = -2x2 + 4x + 2
3. y = -x2 + 2x + 3
4. y = -2x2 + 4x – 6
5. y = -x2 + 2x – 5

Jawab:

Diketahui:
(xp , yp) = (1,4)
(x , y)  = (0,3)

Ditanyakan: fungsi kuadrat yang akan terbentuk?

Untuk parabola yang mempunyai titik puncak rumus yang berlaku seperti di bawah ini:
y = a(x – xp)2 + yp
y = a (x – 1)2 + 4
3 = a(0 -1)2 + 4
3 = a + 4
a = -1

Fungsi kuadrat yang terbentuk yaitu:
y = a(x – xp)2 + yp
y = -1(x -1)2 + 4
y = -x2 + 2x + 3

Jadi jawabannya yaitu: C

DAFTAR PUSAKA  : https://www.yuksinau.id/fungsi-kuadrat/

FUNGSI IRASIONAL 

Pengertian Irasional

Kata Irasional berasal dari bahasa Latin yaitu “ir”, dari bentuk yang diasimilasikan dari in atau tidak serta rasionalis “akal budi”. Dalam matematika, bilangan irasional adalah bilangan riil yang tidak bisa dibagi (hasil baginya tidak pernah berhenti). Dalam hal ini, bilangan irasional tidak bisa dinyatakan sebagai a/b, dengan a dan b sebagai bilangan bulat dan b tidak sama dengan nol. Jadi bilangan irasional bukan merupakan bilangan rasional.

Contoh:

• Mencari nilai pendekatan

Penyelsaian:

(1,4)2 = 1,96 maka 1,4 dapat dipilih sebagai nilai hampiran. Kemudian, 2 (bilangan yang diakar), di bagi dengan 1,4:

2 : 1,4 = 1,4268

---

Selanjutnya mencari nilai rata-rata:

 = 1, 4143

Nilai pendekatan pertama  adalah 1, 4143

Untuk mendapatkan nilai pendekatan yang lebih baik, gunakan 1, 4143 sebagai nilai hampiran 2 : 1, 4141

 = 1, 4142

Jadi, 1, 4142 adalah nilai pendekatan  sampai dengan 3 tempat desimal.

• Mencari nilai pendekatan

(1,7)2 = 2,89 maka 1,7 dapat dipilih sebagai nilai hampiran. Kemudian, 3 (bilangan yang diakar) dibagi dengan 1,7 :

    3:1,7 = 1,7647

---

Selanjutnya mencari nilai rata-rata :

 = 1,73235

1,73235 dipilih sebagai nilai hampiran baru

---

3 : 1,73235 = 2, 73175

 = 1, 73205

Nilai pendekatan  adalah 1,73205

Sebagai pengecekan atau pemeriksaan ulang, kuadratkan 1,73205

(1,73205)2 = (1,73205) . (1,73205) = 2, 9999972025

Yang mana diperoleh hasil penguadratan yang “sangat dekat” atau “hampir sama” dengan 3.

---

Tindakan Ekonomi Irasional

Tindakan ekonomi irasional merupakan tindakan seorang manusia dimana menurut suatu perkiraan akan lebih baik atau menguntungkan namun kenyataannya justru sebaliknya “merugikan”.

---

• Conotoh

Dari tindakan irasional : Antonius pergi bermain dengan mengendarai sepeda motor padahal jarak yang ingin dia tuju hanya 2km dengan beralasan akan lebih cepat  dan praktis serta biayanya murah dibandingkan dengan mengendarai sepeda. Padahal jika diperhitungkan dengan ongkos yang dipakai akan lebih boros mengendarai sepeda motor.

---

Bilangan Irasional

Dalam matematika, sebuah bilangan irasional merupakan bilangan riil yang tidak dapat dibagi (hasil dari bagainya tidak pernah berhenti). Hal tersebut, bilangan irasional tidak dapat dinyatakan sebagai a/b, dengan a dan b sebagai bilangan yang bult dan b tidak sama dengan nol. maka bilangan irasional bukan bilangan rasional.

Menentukan Nilai Aproksimasi Akar Pangkat Dua Suatu Bilangan

Menarik akar pangkat dua suatu bilangan rasional n, akan menghasilakan suatu bilangan rasional, apabila bilangan itu merupakan suatu kuadrat bilangan rasional. Apabila n bukan kuadrat dari suatu bilangna rasional, maka haslnya adalah suatu bilangan irrasional.

---

Menentukan nilai aproksimasi akar pangkat dua dari bilangan yang bukan merupakan kuadrat pangkat dua bilangan rasional, dapat dilakukan dengan 3 cara;

---

• Cara pertama

Cara ini dilakukan seperti mencari akar suatu bilangan dengan cara biasa.

---

• Cara kedua

Misalkan kita ingin mencari nilai aproksimasi dari

3  terletak antara 1² dan 2² atau 1 < 3 < 4, jadi 1<  < 4. Selanjutnya:

(1,7)²= 2,69<3<3,24=(1,8)², jadi 1,7<  < 1,8

(1,73)²= 2,9929<3<3,0276=(1,74)², jadi 1,73<  < 1,74

(1,732)²= 2,99824<3<3,003289=(1,733)², jadi 1,732<  < 1,733

(1,73205)²= 2,9999972<3<3,001704=(1,7321)², jadi 1,73205<  < 1,7321

Dengan melakukan cara ini terus menrus, maka akan diperoleh nilai aproksimasi ang mendekati

Contoh soal: pertidaksamaan irasional tipe jenis ( c )

Pembahasan: 

Contoh soal: pertidaksamaan irasional tipe jenis ( b )

Pembahasan: 

Contoh soal: Pertidaksamaan irasional tipe jenis ( a )

Pembahasan: 

DAFTAR PUSAKA : https://www.quipper.com/id/blog/mapel/matematika/pertidaksamaan-irasional-dan-rasional-matematika-ipa-kelas-10/