KOMPOSISI FUNGSI DAN INVERS FUNGSI

Nama : Refika Rachmawaty

Kelas : X IPS 1

Absen : 28

KOMPOSISI FUNGSI DAN INVERS FUNGSI

Relasi dan Fungsi

Pengertian Fungsi: Relasi dari himpunan A ke himpunan B disebut fungsi atau pemetaan jika dan hanya jika setiap anggota himpunan A berpasangan dengan tepat satu anggota himpunan B.

Suatu fungsi atau pemetaan dapat disajikan dalam bentuk himpunan pasangan terurut, rumus, diagram panah, atau diagram cartesius. Fungsi f yang memetakan himpunan A ke himpunan B ditulis dengan notasi:

$f:A \rightarrow B$

Dengan:

A disebut domain (daerah asal) dinotasikan $D_f$
B disebut Kodomain (daerah kawan) dinotasikan $K_f$

${y \epsilon B \mid(x,y) \epsilon R, x \epsilon A}$ disebut range (daerah hasil), dinotasikan dengan $R_f$ Sebagai contoh:

Contoh 1	Contoh 2	Contoh 3

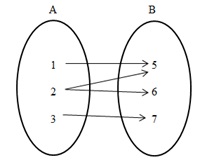
Bukan fungsi karena terdapat anggota di A yang tidak dihubungkan dengan anggota di B	Bukan fungsi karena terdapat anggota di A yang dihubungkan lebih dari satu dengan anggota di B	Meupakan fungsi karena setiap anggota di A tapat dihubungkan dengan satu anggota di B

Sifat-sifat Fungsi

Fungsi surjektif Pada fungsi $f:A \rightarrow B$ , jika setiap elemen di B mempunyai pasangan di A atau $R_f = B$ , atau setiap $y \epsilon B$ terdapat $x \epsilon A$ sedemikian sehingga $f(x) = y$ . Contoh:
- Fungsi Into
Pada fungsi $f:A \rightarrow B$ , jika terdapat elemen di B yang tidak mempunyai pasangan di A.
Contoh:
- Fungsi Injektif
Pada fungsi $f:A \rightarrow B$ , jika setiap elemen di B mempunyai pasangan tepat satu elemen dari A.
Contoh:
- Fungsi Bijektif
Jika fungsi $f:A \rightarrow B$ merupakan fungsi surjektif sekaligus fungsi injektif.
Contoh:

Fungsi Komposisi

Fungsi komposisi merupakan susunan dari beberapa fungsi yang terhubung dan bekerja sama.

Sebagai ilustrasi jika fungsi f dan g adalah mesin yang bekerja beriringan. Fungsi f menerima input berupa (x) yang akan diolah di mesin f dan menghasilkan output berupa $f(x)$ . Kemudian $f(x)$ dijadikan input untuk diproses di mesin g sehingga didapat output berupa $g(f(x))$ .

Ilustrasi tersebut jika dibuat dalam fungsi merupakan komposisi g dan f yang dinyatakan dengan $g o f$ sehingga:

$(g o f)(x) = g(f(x))$

dengan syarat: $R_f \cap D_g \not= {\O}$ .

fungsi komposisi

Komposisi bisa lebih dari dua fungsi jika $f:A \rightarrow B$ , $g:B \rightarrow C$ , dan $h:C \rightarrow D$ , maka $h o g o f:A \rightarrow D$ dan dinyatakan dengan:

$(h o g o f)(x) = h(g(f(x)))$

Sifat-sifat fungsi komposisi:

Operasi pada fungsi komposisi tidak besifat komutatif $(g o f)(x) \not= (f o g)(x)$

Operasi bersifat asosiatif: $(h o g o f)(x) = (h o(g o f))(x) = ((h o g) o f)(x)$

Contoh:

Jika $f(x) = 2x + 3$ dan $(f o g)(x) = 2x^2 + 6x - 7$ , maka g(x) adalah

$(f)(g(x)) = 2x^2 + 6x - 7$

$2(g(x)) + 3 = 2x^2 + 6x - 7$

$g(x) = x^2 + 3x - 5$

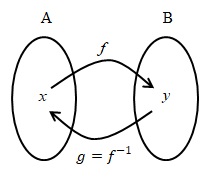
Fungsi Invers

Jika fungsi $f:A \rightarrow B$ memiliki relasi dengan fungsi $g:B \rightarrow A$ , maka fungsi g merupakan invers dari f dan ditulis $f^{-1}$ atau $g = f^{-1}$ . Jika $f^{-1}$ dalam bentuk fungsi, maka $f^{-1}$ disebut fungsi invers.

fungsi invers

Menentukan Invers

Menentukan invers suatu fungsi $y = f(x)$ dapat ditempuh dengan cara berikut:

Ubah persamaan $y = f(x)$ ke dalam bentuk $x = f(y)$

Gantikan x dengan $f^{-1}(y)$ sehingga $f(y) = f^{-1}(y)$

Gantikan y dengan x sehingga diperoleh invers berupa $f^{-1}$

Contoh:

Menentukan invers dari $=x^2 - 2x + 4$ :

$y = [x^2 - 2x + 4$

$y = (x - 1)^2 + 3$

$(x - 1)^2 = y - 3$

$x - 1 = \pm \sqrt{y - 3}$

$x = \pm \sqrt{y -3 + 3}$

Sehingga inversnya adalah

$f^{-1}(x) =\pm \sqrt{y - 3 + 1}$ dan bukan merupakan fungsi karena memiliki dua nilai.

Rumus Fungsi Invers

JENIS FUNGSI	f(x)	$f^{-1}(x)$
Fungsi linier	$f(x) = ax + b$	$f^{-1}(x) = \frac{x-b}{a}$
Fungsi pecahan linier	$f(x) =\frac{ax+b}{cx+d}$	$f^{-1}(x) = \frac{-dx+b}{cx-a}$
Fungsi Irrasional	$f(x) =\sqrt[n]{ax+b}$	$f^{-1}(x) = \frac{x^n-b }{a}$
Fungsi eksponen	$f(x) = a^x$	$f^{-1}(x) = ^a\log x$
Fungsi logaritma	$f(x) = ^a\log x$	$f^{-1}(x) = a^x$

Contoh

JENIS FUNGSI	$f(x)$	$f^{-1}(x)$
Fungsi linier	$f(x) = 2x+3$	$f^{-1}(x) = \frac{x-3}{2}$
Fungsi pecahan linier	$f(x) = \frac{2x+3}{4x+5}$	$f^{-1}(x) = \frac{-5x+3}{4x-2}$
Fungsi Irrasional	$f(x) = \sqrt[4]{2x+3}$	$f^{-1}(x) = \frac{x^4-3}{2}$
Fungsi eksponen	$f(x) = 2^x$	$f^{-1}(x) = ^2\log x$
Fungsi logaritma	$f(x) = ^2\log x$	$f^{-1} = 2^x$

Invers dari Fungsi Komposisi

invers dari fungsi komposisi

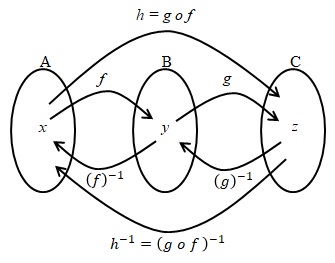
Berdasar gambar, jika f, g, h adalah fungsi dengan contoh $f(x) = 2x + 3$ , $g(x) = 3x - 5$ , dan $h(x) = x =1$ .

Jika $f^{-1},g^{-1},h^{-1}$ adalah invers fungsinya yaitu $f^{-1}(x) = \frac{x-3}{2}$ , $g^{-1}(x) = \frac{x+3}{3}$ , dan $h^{-1}(x) = x - 1$ , maka dirumuskan beserta contohnya:

$(g \circ f)^{-1}(x) = (f^{-1} \circ g^{-1})(x)$

$(g \circ f)^{-1}(x) =f^{-1}(g^{-1}(x))$

$(g \circ f)^{-1}(x) = \frac{(g^{-1}(x))-3}{2} = \frac{\frac{x+5}{3}-3}{2} = \frac{\frac{x-4}{3}}{2} = \frac{2x-8}{3}$

$(f \circ g)^{-1}(x) = (g^{-1} \circ f^{-1})(x)$

$(f \circ g)^{-1}(x) = g^{-1}(f^{-1}(x))$

$(f \circ g)^{-1}(x) = \frac{\frac{x-3}{2}+5}{3} = \frac{\frac{x+7}{2}}{3} = \frac{3x+21}{2}$

$(h \circ g \circ f)^{-1}(x) = (f^{-1} \circ g^{-1} \circ h^{-1})(x)$

$(h \circ g \circ f)^{-1}(x) = f^{-1}(g^{-1}(h^{-1}(x)))$

$(h \circ g \circ f)^{-1}(x) = f^{-1} (\frac{(x-1)+5}{3}) = f^{-1} (\frac{x+4}{3})$

$(h \circ g \circ f)^{-1}(x) = \frac{(\frac{x+4}{3})-3}{2} = \frac{(\frac{x-5}{3})}{2} = \frac{2x-10}{3}$

$(f \circ g \circ h)^{-1}(x) = (h^{-1} \circ g^{-1} \circ f^{-1})(x)$

$(f \circ g \circ h)^{-1}(x) = h^{-1} (g^{-1}(f^{-1}(x)))$

$(f \circ g \circ h)^{-1}(x) = h^{-1}(\frac{3x+21}{2})$

$(f \circ g \circ h)^{-1}(x) = (\frac{3x+21}{2}) - 1 = \frac{3x+19}{2}$

Berdasarkan rumusan tersebut, dapat diturunkan operasi komposisi fungsi sebagai berikut:

Jika diketahui $g(x)$ dan $(f \circ g)(x)$ atau $(g \circ f)(x)$ , maka $(f \circ g \circ g^{-1})(x) = (g^{-1} \circ g \circ f)(x) = f(x)$
Jika diketahui $f(x)$ dan $(f \circ g)(x)$ atau $(g \circ f)(x)$ , maka $(f^{-1} \circ f \circ g)(x) = (g \circ f \circ f^{-1})(x) = g(x)$
Jika diketahui $f(x)$ , $g(x)$ , dan $(f \circ g \circ h)(x)$ , maka $(f \circ g)^{-1}((f \circ g \circ h)(x))$
Jika diketahui $f(x)$ , $h(x)$ , dan $(f \circ g \circ h)(x)$ , maka $f^{-1}((f \circ g \circ h)(h^{-1}(x)))$